HOME --------LIBRARY--------BIOMECHANICS-------- ARCHER FORM--------COACHING--------TECHNICAL--------EQUIPMENT--------MEMBERS--------CONTACT ME

BIOMECHANICS, AND OPTIMIZING PERFORMANCE

In discussing biomechanics at it applies to Archery performance, we are discussing the efficiency of drawing and holding the bow, and aligning the body to provide optimum results while minimizing the adverse stresses and wear on the body. This involves two levels of analysis: Macro scale and Micro scale.

Macro scale analysis looks at the whole body. Computer models of the anatomy are constructed, and used to analyze overall form and alignment and determine the muscular and skeletal loads for each action and at anchor and release. The archer model can be merged with the bow/arrow model to determine how critical each facet of alignment is to arrow flight, and the consequences of misalignment

Micro scale analysis looks at the individual joints, tendons, and ligaments. These are critical because improper motion, loading, and wear, on a joint can cause problems, down stream, after years of practice. Archers will perform the same action up to 100,000 times per year, and the opportunity for repetitive stress injuries is great. This analysis is also important for accommodating para-atheletes as well as archers with bodily variations and injuries.

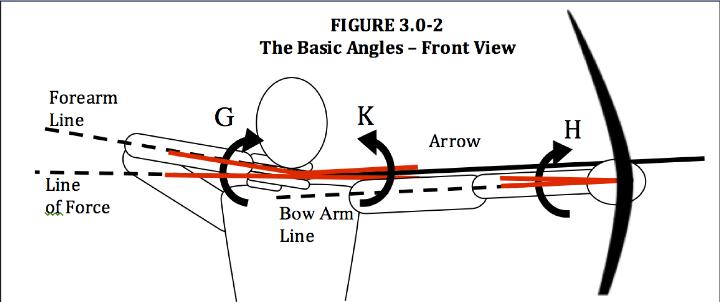
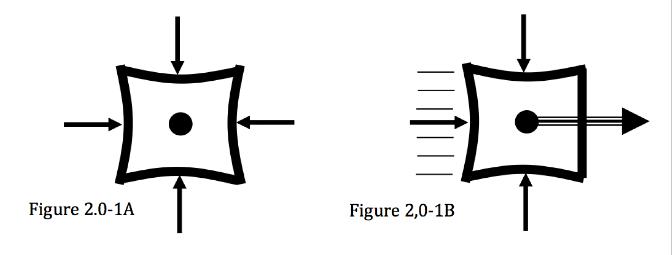
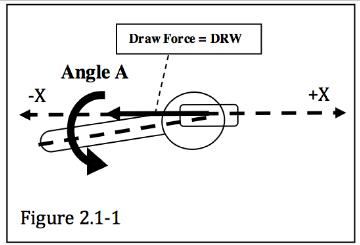
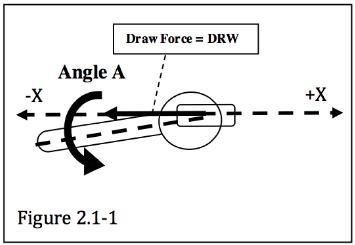
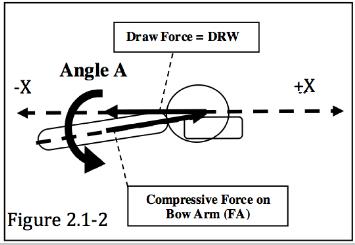
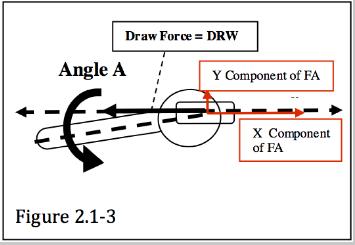
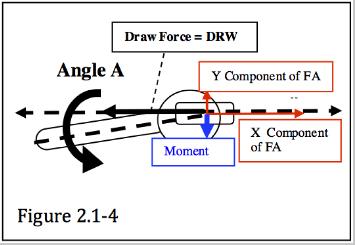
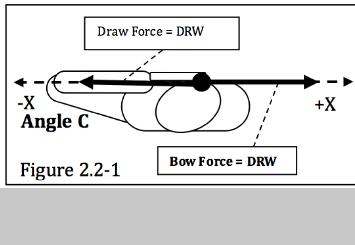
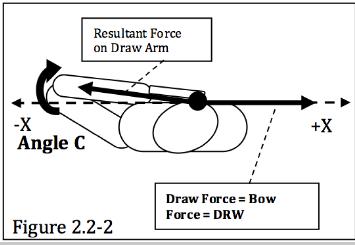
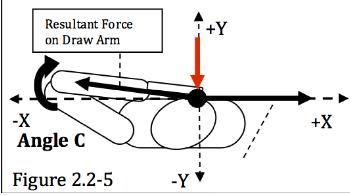
1.0 - MACRO SCALE ANALYSIS:

Macro scale modeling looks at the body as a machine. In this machine, bones are structural members, joints are hinges, and muscles are cables that apply forces to support the skeleton. The skeletal structure can handle loads in compression (pushing) and tension (pulling). As levers, bones can also support a bending moment about a joint. But these bones require muscles to support the basic structure as well as any misalignment, moment, or movement.

Bones can only move by pivoting at joints. Linear motion can be accomplished, but only through coordinated rotations of multiple skeletal members about multiple joints.

Muscles are the motor that drives the system, but they can only be applied in tension. Muscular action can pull directly but can only cause a ‘push’ when it works in conjunction with a skeletal member acting as a lever.

The muscles are often attached to the skeletal structure at very short distances from the joints, or lever points. By pulling on these very close contact points the muscles operate long lever arms. This results in a very poor mechanical advantage, and makes it very important to align the body to put most loads directly into skeletal compression or tension and only use muscular support in a manner that gives an optimal mechanical advantage.

Ultimately these physiological characteristics are what determine the principles of proper shooting form.

2.0 - BASIC CONCEPTS OF STATICS AND MACRO ANALYSIS:

(Note: This section tries to introduce the basics of a entire semester course in Engineering Statics. Its goal is only to introduce the concepts. A more detailed explanation of this topic requires in depth instruction and is far beyond the scope of this introductory presentation.)

Essentially, when an archer is at full draw, he is like the teams in a tug-o-war, in a static position. Actually he is moving slightly as he pulls through the clicker, but for all practical purposes, he is stationary, and every part of the body is static too. This means that all of the muscular tensions and bow forces are balanced at every portion of the body.

The basic concept of Statics is very simple. It says that in a stationary (or ‘static’) body, all of the forces must balance out in all directions (Figure 2.0-1A). Any imbalance in forces would cause movement/acceleration in the direction of the imbalance (Figure 2.0-1B).

Translating this into real life, imagine pushing against a parked car with its brake on. The person pushes against the car, and the car pushes against the road, which pushes back against the car, which pushes back against the person, and everything stays still. If the brake is released then the wheels are free to roll, the road stops pushing back against the car, the car stops pushing back against the person, and the car and person move forward.

Another example, that is more applicable to archery, is two teams competing in a tug-o-war. As long as each team is pulling with equal force, in opposite directions, the system remains stationary. If one team pulls harder, the system moves in that direction. If the rope breaks, both teams fall back in the directions they were pulling at the time of the break.

Let’s take a look at some specific joints to put this thinking process into action.

2.1 - Example 1 – The Bow Hand, at anchor

A line of force exists from the grip at the bow hand to the nocking point, where the draw hand is. The archer is applying a force to the bow at these two points ad the bow is applying a force on the archer, equal and opposite, at the same points.

At the grip, the bow is pushing against the bow hand, and the bow hand is pushing back against the bow. If it were possible to have the bow arm straight in line with the line of force of the bow, that would be the end of this discussion. But, to gain clearance, there must be an angle between the bow arm and the line of force of the bow. This causes a complexity.

We’ll start by ignoring this angle, and just assuming all forces are along the X-axis. We set up the axis system so the bow force is in the –X direction (Figure 2.1-1).

2.1 - Example 1 – The Bow Hand, at anchor

A line of force exists from the grip at the bow hand to the nocking point, where the draw hand is. The archer is applying a force to the bow at these two points ad the bow is applying a force on the archer, equal and opposite, at the same points.

At the grip, the bow is pushing against the bow hand, and the bow hand is pushing back against the bow. If it were possible to have the bow arm straight in line with the line of force of the bow, that would be the end of this discussion. But, to gain clearance, there must be an angle between the bow arm and the line of force of the bow. This causes a complexity.

We’ll start by ignoring this angle, and just assuming all forces are along the X-axis. We set up the axis system so the bow force is in the –X direction (Figure 2.1-1).

In order to balance this force out, the bow hand must be pushing against the bow with an equal force in the +X direction (Figure 2.1-2).

That’s easy enough, but there is a problem here. The bow arm is at a slight angle to the X-axis (Figure 2.1-3). The arm pushes at this slight angle, so that most of its force is pushing in the +X direction, but some of its force is pushing to the side of the X-axis in the Y direction (Figure 2.1-3). So, in balancing things along the X-axis an imbalance is created in the Y direction.

In order to handle this we must break all forces into an X component and a Y component and then we set up equations to balance out the X and the Y components independently, as shown in Figure 2.1-3. The arm is pushing in both the X and Y dimensions but the bow is pushing against the hand along the X-axis, only. There is no Y component to this bow force.

The arm force components are determined by the following equations:

F(X-arm) = F(arm) * COS (A)

F(Y-arm) = F(arm) * SIN (A)

Note that the smaller angle A is, the more the arm force pushes in the X direction and the less the arm force pushes in the Y direction.

With the standard bow and compressive arm force it is easy to balance the forces in the X direction but this leaves a force in the +Y direction that wants to move the bow hand to the front of the archer. This force must be balanced by a force in the –Y direction. This force is applied by a moment (torque) by the bow arm about the bow shoulder. Simply put, the archer pulls back with his arm to balance this force out (Figure 2.1-4).

In the end, all of the forces in the +/– X direction must balance out and all of the forces along the +/- Y direction must also balance out. This must occur for the overall body and for each individual joint.

2.2 - Example 2 – The Draw Hand

When the archer is properly in line, the string is pulling against the hand, in the +X direction, and the hand is pulling back against the string in the –X direction (Figure 2.2-1).

When the archer is not in line and there is an angle C at this point? (Figure 2.2-2)

There must be some lateral loading to support the bend.

Let’s demonstrate this by looking at a simple string in tension. Under normal tension the string is pulled straight (Figure 2.2-3). In order for there to be a bend in the string, there must be a lateral force applied at the point of the bend (Figure 2.2-4).

It is the same with the archer’s arm. The bow is pulling along the X-axis but the arm is pulling at an angle to the X-axis (Figure 2.2-5).

There must be a force that creates the bend. But all forces must be balanced, or else there would be movement. In this case, the balance force comes from the pulling force of the draw arm (Figure 2.2-5).

From our previous discussion about the bow hand, we know that the arm is pulling in both the X direction and the Y direction. The X component of the arm force can be made to balance the X component of the bow force. The force in the Y direction determines the magnitude of the lateral force to pull in, and balance, the system along the Y axis (Figure 2.2-6).

(Figure 2.2-7) So, in this case, the hand is being pulled in (-Y direction – Blue) by a moment about the elbow. It is being matched by a force pulling out in line with the Y component of the draw force of the forearm (+Y direction = Red).

Along the X-axis, the X-component of the force of the draw arm matches the draw force of the bow (Figure 2.2-7).

2.3 - 3-Axis Balance

For simplicity we have been discussing this in the XY plane, but there is also a Z axis and a Z (or vertical) component to each force too. In order to model the archer 3-dimensionally, this angle must also be considered. We are ignoring this 3rd dimension in this discussion to keep the concept simple. However, in computer modeling, the 3 dimensions are always considered.

2.4 - Statics Summary

As stated earlier, this is a very brief introduction into the concepts of statics. We presented only the features that might shed some light on the biomechanics presented in this website. A full discussion of this topic would be prohibitively long for this website.

The basic principle of statics is - In a static or stationary body, all forces must be balanced in all directions. For an archer, this means, if all forces are directly aligned, there are no adverse lateral forces. However, if any angles exist, between the Bow’s line of force and the Archer’s force, this will create an adverse lateral force, and additional body forces must be applied to support and balance these angles.

3.0 – EFFICIENT SKELETAL LOADING

At full draw, the archer should be aligned so that the bow arm is in direct compression, as much as possible. This means that the Radius bone in the forearm is set directly into the pressure point on the bow handle. This ensures that the bow pushes directly into the hand and forearm. The elbow is straight, ensuring that the forearm pushes directly into the Humerus bone of the upper arm, and the Humerus is extended, straight in line with the shoulder line, to take the load directly and compressively into the body.

All alignment should strive to handle loads directly through skeletal members, as much as possible, in direct compression (bow arm and shoulder). All angles should be as small as possible to ensure minimal lateral stresses, since adverse lateral stresses must be handled through a torque applied about a joint.

To study the archer mechanically, it is necessary to model the archer mathematically. Structurally the archer can be analyzed like any other frame structure. Figures 3.0-1 & -2 show the basic archer and labels the 8 critical angles for archer alignment. For a detailed description of each angle and their effect, refer to the manual, “0500 The Wedge”.